Project 4: Constructing Colossi

Purpose

1. Get practice with material that will be on the Blue Belt Exam including: recursive definitions, procedures, lists, asymptotic notation, and analyzing procedures.

2. Learn about cryptography and the first important problems that were solved by computers.

Preparation

Before doing this project, you are expected to have read Chapter 7: Cost of the coursebook, and completed Lesson 5: How Programs Run of Udacity CS101.

Collaboration Policy

This problem set is intended to help you prepare the Blue Belt Exam. You may work on it by yourself or with any number of other students of your choice, but you will need to do the exam on your own. If you work with others, you should turn in one assignment with everyone's name on it, but it is required that everyone understand everything in the submission you turn in.

Regardless of whether you work alone or with a partner, you may discuss the assignment with anyone you want and get help from others, so long as it is help in the spirit of learning how to do things yourself not getting answers you don't understand. You should understand everything you turn in for the assignment well enough to be able to produce it completely on your own.

Remember to follow the course pledge you read and signed at the beginning of the semester. For this assignment, you may consult any outside resources, including books, papers, web sites and people, you wish except for materials from previous cs1120 courses or direct solutions to the given problems. You may consult anyone you want, but that person cannot type anything in for you and all work must remain your own and outside sources should never give you specific answers to problem set questions.

If you use resources other than the class materials, lectures and course staff, you should document this in your turn-in.

As usual, you are strongly encouraged to take advantage of the cs1120 slack group and the scheduled office hours.

Background

Cryptography means secret writing. The goal of much cryptography is for one person to send a message to another person over a channel that an adversary may be eavesdropping on without the eavesdropper understanding the message. We do this by having functions that encrypt and decrypt messages. The encrypt function takes a plaintext message and produces a ciphertext message. Encrypt scrambles and alters the letters of the plaintext message so that an eavesdropper will not be able to understand the message. The decrypt function takes a ciphertext message and produces the corresponding plaintext message. Encryption works as intended if the only person who can perform the decrypt function is the intended recipient of the message.

Since making up good encrypt and decrypt functions and keeping them secret is hard, most cryptosystems are designed to be secure even if the encryption and decryption algorithms are revealed. The security relies on a key which is kept secret and known only to the sender and receiver. The key alters the encryption and decryption algorithm in some way that would be hard for someone who doesn't know the key to figure out. If the sender and receiver use the same secret key we call it a symmetric cipher. If the sender and receiver can use different keys we call it an asymmetric cipher.

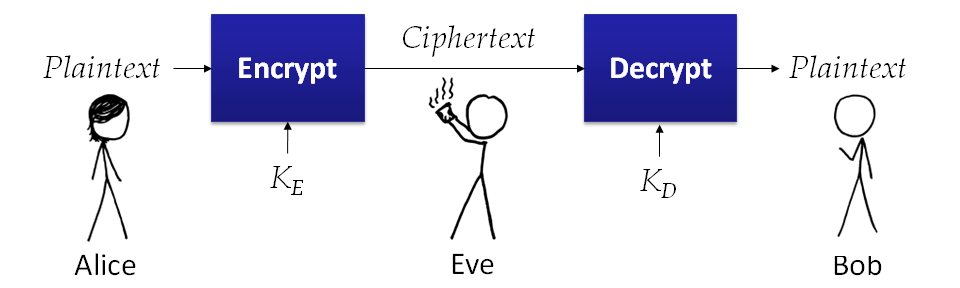
Ciphertext = Encrypt(K_E, Plaintext)
Plaintext = Decrypt(K_D, Ciphertext)

If K_E == K_D it is symmetric encryption.
If K_D cannot (feasibly) be derived from K_D it is asymmetric ("public key") encryption.

In this project, you will explore a symmetric cipher based on the Lorenz Cipher that was used by the German Army High Command to send some of the most important and secret messages during World War II. The Lorenz Cipher was broken by British Cryptographers at Bletchley Park. Arguably the first electronic programmable computer, Colossus, was designed and built by Tommy Flowers, a Post Office engineer working at Bletchley Park during the war. (There is a lot of arguing about what should be considered the first computer. Who Invented the Computer? The Legal Battle That Changed Computing History supports John Atanasoff's case; this Scientific American post summarizes some of the other candidates.) Ten Collosi were built in 1943 and 1944, and used to break some of the most important German messages during World War II. Messages broken by Colossus were crucial to the D-Day invasion since the allies were able to learn that their campaign to deceive Hitler about where the attack would come was succeeding and knew where German troops were positioned.

Bletchley Park (Summer 2004)

Project 4 Repository

Set up your project4 repository in the same way as you did for project 3.

• Fork Project 4. Visit https://bitbucket.org/cs1120/project4/fork. Make sure to check the "This is a private repository" box to make your forked repository private (only visible to yourself and people you authorize to access it). If you are working with partners, just one of you should fork the repository. Then, add the other partners' bitbucket ids to have access to it.

• Clone to your machine. To have a working copy of the repository on your machine, clone the forked repository in SourceTree by selecting File | New/Clone and enter the URL of the cloned repository. You can copy this from the project page you see in bitbucket.org afer forking the provided Project 4 repository. It should be a URL like https://<your bitbucket id>@bitbucket.org/<your bitbucket id>/project4.git. If you are working with partners, all partners should clone the forked repository, so you each have a local copy of it and can play around with the code without interfering with the other partners' copies. (For this project, you should still work together when you work on the code and all partners should be involved in writing all the code. In general, though, using git allows many people to work on the same code and share their changes, and handle conflicts when two people edit the same file.)

The project4 repository contains these files:

• project4.py — A template for your answers. You should do the problem set by editing this file.

• lorenz.py — A few helpful definitions for this problem set, including code to convert between characters and baudot codes, the machine wheel definitions, and ciphertext to break.

Unlike the first three projects, the only code we are providing for this one is tedious code for converting characters to Baudot codes that you could have written yourself, but probably in a more tedious way than is doing by the provided code. You will be writing all of the interesting code yourself for this project.

Measuring Cost

For each of the following subquestions, you will be given two functions, g and f that each take a single parameter n (which must be a non-negative integer) and asked to determine which of O(f(n)), Ω(f(n)), and Θ(f(n)) contain g. It is (of course!) possible that more than one of the sets contain g.

In addition to identifying the properties that hold, you should justify your answer by:

• For each property that is true, select c and n₀ values and show why the necessary inequality holds for all n > n₀.

• For each property that is false, explain why no such c and n₀ values exist. One way to do this is to show how for any selected c value, you can find infinitely many n values that fail to satisfy the necessary property.

For example, if g is n² and f is n³ you would argue:

1. n² is in O(n³) since if we pick c = 1 and n₀ = 1 then n² ≤ cn³ for all n > 1.

2. n² is not in Ω(n³) since for any c value we know n² is not greater or equal to cn³ for all n > 1/c. This is the case since we can simplify the inequality to 1 ≥ cn which is not true if we choose n > 1/c.

3. n² is not in Θ(n³) since n² is not in Ω(n³).

The Exclusive Or (XOR)

The exclusive-or (xor, sometimes pronounced "zor") function is every cryptographers favorite function. The xor function takes two Boolean inputs, and returns True if exactly one of the inputs is True, and returns False otherwise. Often in English, when people say "or", what they really mean is "xor". For example, when someone asks "Would you like the chicken or fish?", they do not consider "both" to be a valid answer.

In cryptography, it is usually easier to deal with the binary digits 1 and 0 instead of True and False. We use 1 to represent true and 0 to represent false, and call each 0 or 1 a bit. (The term bit was introduced by Claude Shannon.)

Your xor function should produce these interactions:

 
>>> xor(0,0)
0 
>>> xor(0,1) 
1 
>>> xor(1,0) 
1 
>>> xor(1,1)
0 

The xor function has several properties that make it extremely useful in cryptography:

• invertibility — xor(xor(a, b), b) == a. No matter what b is, xor-ing any value with it twice results in the original value. This means if we encrypt a message by xor-ing it with a key k, we can decrypt the message by just xor-ing it again with the same key!

• perfect secrecy — if m is a message bit and r is a perfectly random bit (equally likely to be 0 or 1), then the probability that xor(m, r) == 0 is 1/2, regardless of m.

The second property means that if a message is encrypted by converting the message into a sequence of bits, and xor-ing each bit in the message with a perfectly random, secret bit known only to the sender and receiver, then we can send a message with perfect secrecy! This is known as a one-time pad (and is, essentially, the only perfect cipher possible, as was proven by Claude Shannon).

Fortunately for the Allies, the Nazis did not have a way of generating and distributing perfectly random bit sequences. Instead, they generated non-random sequences of bits using rotors. Because the sequences of bits generated was determined by the structure of the machine used to generate them, the Allies were able to figure out a way to break the code.

We will look at how the Lorenz cipher used xor to encrypt messages soon, but first, consider how to turn messages into sequences of bits.

The Baudot Code

The Nazis used the Baudot code to represent the letters in their messages as sequences of bits. The Baudot code translates letters and other common characters into a 5-bit sequences. With five bits, we have 2⁵ = 32 possible values. This is enough to give each letter in the alphabet a different code and have a few codes left over for spaces and other symbols.

Table 1 shows the letter mappings for the Baudot code. For example, the letter H is represented by 10100 and I is 00110.

We can put letters together just by concatenating their encodings. For example, the string 'HI' is represented in Baudot as 1010000110.

There are some values in the Baudot code that are awkward to print: carriage return, line feed, letter shift, figure shift and error. For our purposes we will use printable characters unused in the Baudot code to represent those values so we can print encrypted messages as normal strings. Table 1 shows the replacement values in parenthesis.

We can use lists of bits to represent Baudot codes. H is represented as the list [1, 0, 1, 0, 0]. A string is represented as a list of these lists: 'HI' is [[1, 0, 1, 0, 0], [0, 0, 1, 1, 0]].

We have provided two functions in lorenz.py:

char_to_baudot(char): Character → Baudot

Takes a character as input, and outputs the corresponding Baudot code represented as a list of five bits.

baudot_to_char(bcode): Baudot → Character

Takes a baudot code, represented as a list of five bits, as input and outputs the corresponding character.

Your string_to_baudot and baudot_to_string functions should be inverses. Hence, you can test your code by evaluating compositions like, baudot_to_string(string_to_baudot("HELLO")) (which should return "HELLO").

Lorenz Cipher Machine

The Lorenz Cipher

The Lorenz cipher was an encryption algorithm developed by the Germans during World War II. It was used primarily for communications between high commanders in Axis headquarters and conquerer capitals. The original Lorenz machine consisted of 12 wheels, each one having 23 to 61 unique positions. Each position of a wheel represented either a 0 or a 1.

The first 5 wheels were called the K wheels. Each bit of the Baudot representation of a letter was xor-ed with the value showing on the respective wheel.

The same process was repeated with the next 5 wheels, named the S wheels. The resulting value represented the encrypted letter.

After each message letter the K wheels turn one rotation. All five of the wheels advance one position (this coordination of movement across the wheels is one of the biggest weaknesses in the cipher design).

The movement of the S wheels was determined by the positions of the final two wheels, called the M wheels.

Lorenz Cipher Wheels

Like most ciphers, the Lorenz machine also required a key. The key determined the starting position of each of the 12 wheels. To decipher the message you simply need to start the wheels with the same position as was used by the sender to encrypt the message, and enter the ciphertext. Because of the invertability of xor, when the receiver's machine produces the same sequence of encryption bits the receiver obtains the original message by xoring the ciphertext with the generated bits.

There were 16,033,955,073,056,318,658 possible starting positions. This made the Nazis very confident that without knowing the key (starting positions of the wheels), no one would be able to break messages encrypted using the Lorenz machine. There confidence was futher bolstered by knowing that the Allies had not acquired a single Lorenz machine, since the machines were all kept in highly secure locations controled by the Axis (this is different from Enigma machines which were widely deployed in the field, with every army unit and submarine having one).

Their confidence was misplaced, however, and Allied cryptographers at Bletchley Park were able to deduce the structure of the Lorenz machine from intercepted re-transmissions (with errors), identify statistical weaknesses in the encryption, and build a computer to rapidly decrypt intercepted messages, providing great benefits to the Allies during the last years of the war.

Since the full Lorenz cipher would be too hard for this project, we will implement a simplified version. You should be suitably amazed that the allied cryptographers in 1943 were able to build a computer to solve a problem that is still hard for us to solve today! (Of course, they did have more that a week to solve it, and more serious motivation than we can provide in this course.)

Our Lorenz machine will use 11 wheels, each with only 5 positions. The first five wheels will be the K wheels and the second five the S wheels. Each of these will only have a single starting position for all 5 — that is, unlike the real Lorenz machine, for this project we will assume all five K wheels must start in the same position and all five S wheels must start in the same position.

The final wheel will act as the M wheel. After each letter all the K wheels and the M wheel should always rotate. Before the M wheel rotates, if it shows a 1 the S wheels should also rotate, but if the M wheel shows a 0 the S wheels do not rotate.

Describing the Simplified Lorenz Machine

We have provided 3 lists that represent the wheels in lorenz.py. The first is called K_wheels and is a list of lists, each of the inner lists containing the 5 settings:

K_wheels = [[1,1,0,1,0], [0,1,0,0,1], [1,0,0,1,0], [1,1,1,0,1], [1,0,0,0,1]]

There is a similar list called S_wheels to represent the S wheels of our simulated machine.

S_wheels = [[0,0,0,1,1], [0,1,1,0,0], [0,0,1,0,1], [1,1,0,0,0], [1,0,1,1,0]]

The final list represents the M wheels and is just a single list (it is just one wheel, so is a single list representing that wheel, not a list of wheels):

M_wheel = [0,0,1,0,1]

To rotate our wheels, we will take the number at the front of the list and move it to the back. Thus, the first number in the list represents the current position of the wheel.

We also want a procedure that can rotate a wheel zero or more times:

Next, we define similar functions that work on a list of wheels at a time instead of a single wheel.

Simulating the Lorenz Machine

Now that we can rotate our wheels, we simulate the Lorenz machine using our K and S wheels. Since both sets of wheels are doing the same thing, we should be able to write one procedure that will work with either the K wheels or the S wheels.

Your wheel_encrypt function should have running time in Θ(n) where n is the length of the list passed as the first parameter to wheel_encrypt. Even though our Lorenz crypotography will always involve lists of length five, your answer must work for any length inputs as long as both lists have the same length.

For example, wheel_encrypt([0, 0, 0, 1, 1], K_wheels) should produce [1, 0, 1, 0, 0].

We now have all the procedures we need to implement our simplified Lorenz machine. A quick review of how the machine should work:

• Each of the five bits of the Baudot representation of a letter is xored with the current position of the respective K wheels.

• The resulting five bits from the previous step are xored with the current position of the respective S wheels to produce the ciphertext.

• The K wheels are rotated one position.

• The S wheels are rotated one position only if the value at the current position of the M wheel is 1.

• The M wheel is rotated one position.

This process is repeated for each letter in the message.

For example:

>>> do_lorenz(string_to_baudot("COOKIE"), K_wheels, S_wheels, M_wheel)
[[1, 1, 0, 1, 0], [0, 0, 0, 0, 1], [1, 1, 0, 0, 1], [1, 0, 0, 0, 1], \ 
 [0, 0, 1, 1, 1], [1, 1, 0, 1, 1]]

You should now be able to encrypt strings using the simplified Lorenz cipher. To test it, call your lorenz_encrypt function with a string and offsets of your choice to produce ciphertext. Since our encryption and decryption functions are the same, if you apply lorenz_encrypt again using the ciphertext and the same offsets you should get your original message back:

>>> lorenz_encrypt("CAKE", 1, 2, 3)
"BNR!"
>>> lorenz_encrypt("BNR!", 1, 2, 3)
"CAKE"

Cracking the Code

The first Lorenz-encrypted messages were intercepted by the British in early 1940. The intercepts were sent to Bletchley Park, the highly secret British base set up specifically to break enemy codes. The code-breakers at Bletchley Park had little success with the Lorenz Cipher until the Germans made a major mistake in late 1941. A German operator had nearly finished sending a long message using a Lorenz machine when the receiver radioed back to tell him that the message had not been received correctly. The operator then reset his machine back to the same starting position and began sending the message again. But the operator, probably frustrated at having to resend the message, abbreviated some of the words he had typed out completely the first time. This led to two nearly identical messages encrypted using the same starting positions.

The messages were sent to John Tiltman at Bletchley Park. Tiltman was able to discern both messages and determine the generated key. The messages were then passed on to Bill Tutte who, after two months of work, figured out the complete structure of the Lorenz machine only from knowing the key it generated. The British were then able to break the Lorenz codes, but much of the work needed to be done by hand, which took a number of weeks to complete. By the time the messages were decrypted they were mostly useless.

The problem was given to Tommy Flowers, an electronics engineer from the Royal Post Office. Flowers designed and built a device called Colossus that worked primarily with electronic valves. The Colossus was the first electronic programmable computer. It was able to decrypt the Lorenz messages in a matter of hours, a huge improvement from the previous methods. The British built ten more Colossi and were able to decrypt an enormous amount of messages sent between Hitler and his high commanders. The British kept Colossus secret until the 1970s. After the war, eight of the Colossi were quickly destroyed and the remaining two were destroyed in 1960 and all drawings were burnt. The details of the breaking of the Lorenz Cipher were kept secret until 2000, but are now available at http://www.codesandciphers.org.uk/documents/newman/newmix.htm.

Colossus (Original, 1943)

Colossus (Rebuilt, 2004)

Our simplified cipher will be much easier to break. There are only 5 starting positions for the K wheels, 5 starting positions for the S wheels, and 5 starting positions for the M wheel. Hence, the keyspace for our simplified Lorenz machine is 125. This is a small enough keyspace that it can be broken using "brute force": go through all the possible keys looking for a likely message. Because of the tiny keyspace, no clever cryptanalysis or even automated message recognition is required (unlike what was necessary for the real Lorenz cipher, with an astronomically huge keyspace).

If your procedure works correctly, one of the messages generated will look like sensible English and you will have found the key and message! (Your procedure does not need to return any value, although a more useful procedure would return the most likely plaintext message.)

Anyone who solves the "Triple-Gold-Star Challenge" will be offered a paid summer position in Dave's research group. (A good attempt is also probably worthy of a summer position, but not guaranteed.)